第一百四十一章 11世纪全球最强数算天团!(6.6k)
后世大学阶梯教室的黑板都见过吧?
如果用第四种方法,最少需要六块这种黑板——而且还不一定能算 解析解。
解析解。
所以除非前面的近似理论不适用,否则一般没人这么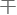 。
。
也正因如此,徐云准备走的是第三种思路。
虽然第二种方式在理论数学上复杂很多,算一个透镜要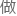 两次二重积分。
两次二重积分。
但一来它的现实效果最好,在理论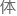 系严重滞后的
系严重滞后的 况
况 ,现实效果的重要
,现实效果的重要 无需多言。
无需多言。
二来便是.....
老贾,他可是杨辉三角的真正发明人。
杨辉三角是解积分最契合一古老工 之一,因此想让老贾踏
之一,因此想让老贾踏 那一步,理论上其实是有不少实
那一步,理论上其实是有不少实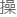
 的。
的。
当然了。
这里的踏 一步并不是指发明微积分,而是一种思路上的暂时
一步并不是指发明微积分,而是一种思路上的暂时 应用。
应用。
毕竟单靠一个杨辉三角是没法鼓捣 来微积分的,需要一定的数学积累才有——更关键的是,这种数学积累指的还不是个人积累,而是整个数学界的积累。
来微积分的,需要一定的数学积累才有——更关键的是,这种数学积累指的还不是个人积累,而是整个数学界的积累。
视线再回归原 。
。
在骤然发现了一个新领域后,老贾和韩公廉等人表现 了相当
了相当 郁的兴致。
郁的兴致。
毕竟这年 ,这种团队公关的
,这种团队公关的 况太少见了。
况太少见了。
只见几人或在讨论思路,或直接上手 行了数据测量。
行了数据测量。
比如刘益的手里,此时便 现了一个很原始的工
现了一个很原始的工 :
:
曲尺。
说 曲尺,就不得不先说另一个概念了:
曲尺,就不得不先说另一个概念了:
角度。
华夏古人在其漫长的科技实践中,其实很早形成了 象角度概念——这里的早字,甚至可以追溯到三四千年前。
象角度概念——这里的早字,甚至可以追溯到三四千年前。
但遗憾的是。
他们并没有以此为发展,建立相应的角度 确计量——注意,是
确计量——注意,是 确计量。
确计量。
这种 况要持续到到明朝,传教士利玛窦带来的角度概念,方才打破了这种局面:
况要持续到到明朝,传教士利玛窦带来的角度概念,方才打破了这种局面:
他和徐光启合作翻译的《几何原本》给 了角的一般定义,描述了角的分类及各种
了角的一般定义,描述了角的分类及各种 况、角的表示方法,以及如何对角与角
况、角的表示方法,以及如何对角与角 行比较。
行比较。
而在此之前。
华夏一般只有两种 略的角度计量方式。
略的角度计量方式。
第一种非常简单,就是只 钝角和锐角划分,用到的字是倨和勾。
钝角和锐角划分,用到的字是倨和勾。
倨表示钝,勾表示锐。
倨勾中矩,就是直角。
而第二种就比较复杂了。
它和测量方位有些类似: