歇尔的那架定义了银河系的反式望远镜。

        面对如此一尊庞然大，哪怕辅助副镜不需要太过细的数据，锻造起来也是非常麻烦的。

        首先便是副镜的曲率问题，这事儿徐云只能亲自手了。

        没办法。

        球差是三阶像差，无法在斯光学的范围表达，更别提现在连斯光学都没接多少的老贾了。

        徐云的计算方案是这样的：

        据赛德尔像差多项式中的球差分，可以写单个薄透镜的球差系数：

        s=（（c1-c2）2n3s  2（c1-1/s）2-（c1-c2）2n2（2c1-3/s）  n(c1-1/s)(c2-3/s))  （y3（1-n）/n）

        这里c1和c2是薄透镜的两个表面的曲率，s是距，y是光线度。

        对于徐云的副镜组来说。

        由于采用薄透镜假设，两个球面透镜上的光线度是一样的。

        从而可以在最终结果里约去这个度。

        而第一个球面镜a的位于无穷远，第二个球面镜b的就是第一个透镜的像。

        所以有sa=∞，sb=∫a。

        徐云之前特意找老苏收集了火石玻璃（见125章），通过制备大蒜素的电解池理，可以得到折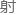率n在1.51680的标准玻璃。

        是的。

        徐云之前在准备制作大蒜素的时候，便考虑到了望远镜的这一步，甚至更远。

        随后把实际参数代求解，便可以得到两组可行解。

        一组是c1=0.000494801mm^-1，c2=-0.00173844mm^-1

        另一组则是c1=0.00107834mm^-1，c2=-0.0011155mm^-1（应该没算错，有算错的话迎指正）

        也就是说。

        合适的玻璃曲率有两种。

        接着再将这两组数据记录转移，套到老贾他们先前算的那个接近1.3的式中。

        便可以得理论上不需要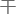涉仪便可以确定的最优曲库模板。

        随后徐云想了想，继续对老苏：

        “老爷，照咱们的预估，副镜的研磨可能需要一个月左右。

        因此接来的日里，可能就需要您和齐师傅他们多辛苦一了。”

        老苏闻言，有些慨的笑了一声：

        “区区旬月而已，若能看清星辰，莫说一月，一年老夫都撑得住！”

        随后他转过，对着另一位五六十岁的小老拱了拱手：

        “倒是齐师傅，这次恐怕要有劳你了。”

        小老连忙回礼：

        “不敢不敢，若非恩公当初援手，小老举家上怕是早已成了路边枯骨，何曾得享今日之福？

        还请恩公莫要多言，否则实乃羞煞小老也。”

        老苏闻言没再说话，而是亲切的拍了拍小老的肩膀。

        这个小老也是制局的一位大师，名叫齐格飞，据说是北宋目前锻造工艺最好的一位匠人。

        当初老苏前往鲁东清账目之时，偶然在路旁遇到了因粮荒逃难的齐格飞。

        当时老苏看他可怜，便本着好心将他带在了边。

        一如当初对徐云那般，打算回京后安排个仆役的差事。

        不过在一次巧合，老苏意外发现齐格飞有着一手不错的工活，甚至要比不少京中工匠还要好。