d/b2可以判断，这应该是一个涉及到旋转曲面的问题。

        第二行的∑(jik=s)∏(jik=q)(xi)(wj)则可以确定曲面与经线成了某个定角。

        既然是定角，那么就可以假设定模型λ=(a，b，π)，以及观测序列o=(o1，o2，...，ot)。

        那么就有α1(i)=πibi(o1)，i=1，2，...，n

        αt  1(i)=[j=1∑nαt(i)aji]bi(ot  1)，i=1，2，...，n

        十五分钟后。

        看着面前的结果，徐云若有所思：

        “极大化的模型参数吗......”

        随后他思索片刻，继续在纸上写了一公式：

        q(λ，λ)=i∑logπi1p(o，i∣λ)  i∑(t=1∑t?1logaitit  1)p(o，i∣λ)  i∑(t=1∑tlogbit(ot))p(o，i∣λ)。

        这是一个很简单的投影曲线，并且圆锥对数螺线上任一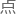的挠率也与该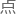到轴的距离成反比。

        因此可以化简成另一个表达式。

        δt(i)=i1i2，...，it?1maxp(it=i，t?1，...，i1，ot，...，o1∣λ)，i=1，2，...，n

        解着解着，徐云的表也愈发凝重了起来。

        两个小时后。

        徐云看着面前的图纸，眉紧紧的拧成一团：

        “好家伙，第一组方程的化解项，居然是一个观测态的方程？”

        观测态方程其实是个很奇怪的玩意儿，它在数学中的释义比较复杂，但在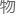理中的释义却很简单：

        它表示着一个时序的非概率模型，指的是状态空间中经过从一个状态到另一个状态的转换的非随机过程。

        看到这里。

        有些同学是不是觉很熟悉？

        没错。

        这是一个定义上与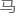尔科夫链完全相反的模型，描述的是一种很小区间的定可能。

        而这种模型，一般只会现在.......

        超级超级小的微观领域。

        想到这里。

        徐云忽然灵光一闪。

        “微观领域，衰变积分？”

        只见他飞快的拿起笔，在其中另一张纸上飞快的写了一行字：

        y(xn  1)?y(xn)/h≈f(xn，y(xn))

        y(xn  1)=y(xn)  hf(xn，y(xn))

        写完这些后。

        徐云拿笔记本，打开了一个定制版的理件。

        这是科大研究生才能申请的量化计算程序，以斯的量化计算为心基础运行，可以计算一些度有限的模型，名字叫极光。

        极光中录了目前已发现的所有微粒的运行轨迹，连接的是科大同辐那边的一台次级服务。

        随后徐云通过mathpix将自己写好的公式识别、传输，了回车键。

        十二秒后。

        一个数字现在了徐云面前：

        0。