第三百三十四章 再见了,1850!(一)(9.8K!!)
镜 以及两者之间连线所构成的整
以及两者之间连线所构成的整 。”
。”
“在任意时刻,光臂的长度是恒定的——或者说在任意时刻,光源和镜 之间的距离是定值。”
之间的距离是定值。”
“这 也没问题吧?”
也没问题吧?”
回答他的依旧是赞同声。
说完这些。
徐云玩味的看了乔吉亚·特里一 ,嘴角抑制不住的微微翘起了一丝弧度:
,嘴角抑制不住的微微翘起了一丝弧度:
“至于这位乔吉亚·特里先生的所谓漏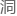 ,实际上可以分成垂直光路和
,实际上可以分成垂直光路和 平光路两
平光路两 分。”
分。”
“虽然他绝大 分的思路是在讨论垂直光路,我们还是要先讨论一
分的思路是在讨论垂直光路,我们还是要先讨论一 他在分析
他在分析 平光路时犯的错误吧,麦克斯韦!”
平光路时犯的错误吧,麦克斯韦!”
一旁的小麦闻言神 一震:
一震:
“在呢,罗峰先生。”
徐云朝他打了个响指,将粉笔朝他一丢:
“小麦,你给这位先生整个活,告诉他他到底错在了哪儿。”
小麦闻言

 ,接过粉笔,又看了
,接过粉笔,又看了 乔吉亚·特里。
乔吉亚·特里。
思索了半分钟左右,他便在黑板上写 了两个式
了两个式 :
:
om1 m1o。
om1 vt1 om1-v(t11-t1)=2om1 v(2t1-t11)
接着在第一个式 后
后 打了个叉。
打了个叉。
在第二个式 后打了个√。
后打了个√。
看着黑板上的两 公式。
公式。
围观群众中的某位数学教授顿时轻轻 了一
了一 气:
气:
“嘶.......”
小麦所写的 容不多,但现场毕竟有着不少真正的数理大老,理解能力方面还是拉满的。
容不多,但现场毕竟有着不少真正的数理大老,理解能力方面还是拉满的。
他们只是稍微一分析,便立刻理解了小麦的想法。
读过 中
中 理的同学应该都知
理的同学应该都知 。
。
一个
 的运动轨迹,在不同参考系中是不同的。
的运动轨迹,在不同参考系中是不同的。
例如假设你在坐火车,你相对于火车的轨迹是一个不动的 。
。
而你相对于地面参考系的轨迹,却是一条直线。
这个 理同样适用于光路。
理同样适用于光路。
以太假设的 心就在于,它认定了光相对于以太的速度是恒定的。
心就在于,它认定了光相对于以太的速度是恒定的。
所以如果想比较两束光从光源击中镜 再回到光源所消耗的时间差,选取以太作为参考系更加方便。
再回到光源所消耗的时间差,选取以太作为参考系更加方便。
小麦的思路便是如此。
当t=0时。
光从光源o
 发。
发。
当t=t1的时候。
光到达镜 。
。
此时由于整个实验设备相对于以太已经向右移动了一段距离,镜 的位置从m1
的位置从m1 变换到了右侧距离vt1的地方。
变换到了右侧距离vt1的地方。
所以这一段光程的长度是:
om1 vt1。
当光返回光源的时候。
设光在t=t11时返回光源,此时光源已经运动了t11秒。
所以光源的位置是原先o 右侧距离vt11的地方。
右侧距离vt11的地方。