第五百五十九章 真给跪了

 :
:
「正合我意。」
于是很快。
钱五师便计算起了背压比。
所谓背压比。
指的 嘴
嘴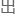
 静压力与
静压力与 嘴上游滞止压力之比,不过在设计方案中指的是锥
嘴上游滞止压力之比,不过在设计方案中指的是锥 场与气
场与气 的耦合比。
的耦合比。
当锥 场刚好达到临界条件时。
场刚好达到临界条件时。
外 气
气 达到音速,同时气
达到音速,同时气 质量
质量 量达到最大值,此时的背压比即称为最大背压比。
量达到最大值,此时的背压比即称为最大背压比。
这个概念有 类似后世的mbpr,不过释义上更接近
类似后世的mbpr,不过释义上更接近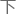 游。
游。
接着很快。
徐云也估量了一番自己的右手状态。
今天他的右手还没用过,负载为0,因此他便也拿起笔和纸协助写了起来。
众所周知。
如果激波为正激波,且不考虑激波厚度,那么激波控制 的形状就会很对称:
的形状就会很对称:
你比划个剪刀的手势,然后指尖向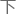 。
。
这就是激波控制 的图示了。
的图示了。
而控制 cv基本方程,则由三个连续方程组成:
cv基本方程,则由三个连续方程组成:
dΦdt=ddt∫v?(r,t)dv=??t∫v?(r,t)dv
s?(r,t)u?nda
Δn=(?iiσd ?iiiσd))t Δt?(?iiσpd)t
lit→0(?iσd)t ΔtΔt=??σ?v→?da→=?σs?αda(这排版将就着看吧)
其中t为时间;
fx为控制
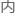

 的受力在x轴上的分量;
的受力在x轴上的分量;
v为
 速度失量;
速度失量;
a为控制 表面面积失量;
表面面积失量;
v为控制
 积。
积。
同时考虑气 稳定
稳定 动,再假设速度、能量在激波截面上是均匀的。
动,再假设速度、能量在激波截面上是均匀的。
便有∫csv·daa。
随后徐云把截面态联立在了一起,准备继续推导 去。
去。
然而半分钟后。
徐云忽然眉 一皱,嘴里啧了一声,轻轻摇了
一皱,嘴里啧了一声,轻轻摇了 :
:
「不行,要是这样
拟合的话,就没法继续计算了.....」
结果话音刚落。
徐云的耳边忽然传来了一 声音:
声音:
「韩立同志,为什么没法继续计算?」
「?」
徐云顿时一怔,顺势朝发声者看去。
转过 后。
后。
发现数算小组的那位被叫 什么「大于」的圆脸中年人,不知何时已经来到了自己
什么「大于」的圆脸中年人,不知何时已经来到了自己 边。
边。
徐云见状扫了 正在低
正在低 计算的钱五师,压低声音解释
计算的钱五师,压低声音解释 :
:
「大于同志,这不是很明显吗?」
「激波后的温度 于激波产生前,压力间断
于激波产生前,压力间断 地急剧上升,扩散段的方程显然是算不
地急剧上升,扩散段的方程显然是算不 来的。」
来的。」
说罢。
徐云便摇了摇 ,准备试着思考另一种方法。
,准备试着思考另一种方法。
然而令他有些意外的是。
圆脸中年人闻言后没有再说话,而是同样低 拿着笔和纸写了起来。
拿着笔和纸写了起来。
徐云见状也不再说什么,继续 起了思考。
起了思考。
过了大概三四分钟。
中年人忽然将算纸递到了徐云面前,说 :
:
「韩立同志,你看看这个。」