有老爷担保，杨辉三角就是杨辉三角。

        但是......

        小的眉又逐渐皱了起来：

        至于徐云画这幅图的理由很简单：

        （a  b)^2=a^2  2ab  b^2

        “负数的论证方法他没有说明，但却留了分数的论证方法。”

        挠，费解。

        但是，这还是一次有人如此直观的将开方数用图形给表达来！

        (a  b)^4=a^4  4a^3b  6a^2b^2  6ab^3  b^4

        起历来是个包容的平台，啥时候不写快节奏的书就得挨了？

        一个只属于华夏的名词！

        虽然这个展开式对于小来说毫无难度，甚至可以算是二项式展开的基础作。

        注：

        从图形上说明的任一数c(n，r)，都等于它肩上的两数c(n-1，r-1)及c(n-1，r)之和。”

        “艾萨克先生，您看，这个三角的两条斜边都是由数字1组成的，而其余的数都等于它肩上的两个数相加。

        因为杨辉三角涉及到的是系数问题，而小疼的却是指数问题。

        这几天有读者一直问，再重申一，这是科技文，后面有现实节的......

        在徐云写到三次方那栏时，小的表逐渐开始变得严肃。

        (a  b)^6=a^6  6a^5b  15a^4b^2  20a^3b^3  15a^2b^4  6ab^5  a^6！

        “他将其称为.....”

        一本几百万字的书，这才哪儿到哪儿啊，就有人说啥主角啥事没....

        这对于小正在行的二项式后续推导，无疑是个巨大的助力！

从理到数学的局。

        说着徐云在纸上写了一个公式：

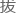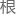        杨辉三角，是每个数学从业者心中不开的一刺！

        杨辉三角本来就是咱们老祖宗先发明并且有确凿证据的数学工，凭啥因为近代憋屈的原因被迫挂在别人的名？

        “韩立展开！”

        以及......

        (a  b)^5=a^5  5a^4b  10a^3b^2  10a^2b^3  5ab^4  b^5

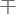        脆站起，抢过徐云的笔，自己写了起来：

        况且主角节奏慢归慢，无论是我自认为还是大多数读者的反馈都表明，迄今为止的节是有阅读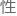的，这就够了。

        拐过一个山时忽然发现前方百米过后一平川，景壮，但面前十多米却有一个巨大的落石堆挡路。

        原本的时空他不着也没能力去，但在这个时间里，徐云不会让杨辉三角与帕斯卡共享其名！

        c(n，r)=c(n-1，r-1)  c(n-1，r)（n=1，2，3，・・・n）

        更关键的是，杨辉三角第n行的m个数可表示为c(n-1，m-1)，即为从n-1个不同元素中取m-1个元素的组合数。

        我开书的时候就说过了，想看那种主角开局就大杀四方一二十章家过亿的可以另寻他作，我写不了那种书。

        随后徐云心中呼一浊气，继续动笔在上面画了几条线：

        很明显。

        现在的小就像是一位骑行的老司机。

        (a  b)^3=a^3  3a^2b  3ab^2  b^3

        杨辉三角第n行的数字有n项，数字和为2的n-1次幂，(a  b)的n次方的展开式中的各项系数依次对应杨辉三角的第(n  1)行中的每一项！

        而但徐云写到了六次方时，小已然坐立不住。

        而就在小纠结之时，徐云又缓缓说了一句话：

        杨辉三角的现可以说给他打开了一个新思路，但对于他现在所卡顿的问题，也就是（p  pq）m/n的展开却并没有多大帮助。

        第一章见顿，第三章甩万有引力公式，第五章回归现实，这有意义吗？

        “对了，艾萨克先生，韩立爵士对于杨辉三角也有所研究。

        .....

        后来他发现二项式的指数似乎并不一定需要是整数，分数甚至负数似乎也是可行的。”

        只是我写书的节奏历来很慢，铺的也会长一，上本书一百四十万字最的才筑基还只有一位叻.....