第二百五十七章 见证奇迹吧！（上）
标准的人话，不难听懂。
栞ⴍ풸噧ൾ迉چ玫嬇펊穏䖂ꗯ蓕涫唸ᖳ�ℍ볹标准的人话，不难听懂。
栞ⴍ풸噧ൾ迉چ玫嬇펊穏䖂ꗯ蓕涫唸ᖳ�ℍ볹 函数就是一种映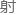
关系，在函数y=f(x)里，每给定一个x，通过一定的
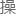作f(x)就能得到一个y。
但是力的作用又是相互的，附近的
给端施加了一个张力，那么这个附近的也会受到一个来自端的拉力。
我们的手只是拽着绳
的一端，并没有碰到绳的中间，但是当这个波传到中间的时候绳确实动了。
于是徐云继续开始了推导。
騠�꿜잿拱鐹⩦엜樨☉絀玕�셒�ܐ㐂 至于波在
个时刻移动了多少也很好计算：
一
绳放在地上的时候是静止不动的，我们甩一就会
现一个波动。
答案同样很简单：
ป厝骞贕ừ嗁ᣔ塽秅锧㉡낯䖒㡟怟쁫鎊䙙， 函数就是一种映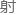关系，在函数y=f(x)里，每给定一个x，通过一定的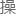作f(x)就能得到一个y。
图像某个的纵坐标y不仅跟横轴x有关，还跟时间t有关，这样的话就得用一个二元函数y=f(x，t)来描述一个波。
绳会动就表示有力作用在它
上，那么这个力是哪里来的呢？
因为波速为v，所以Δt时间以后这个波就会往右移动v·Δt的距离。
짏쀢酭ﱵབ㩨ಾ墊紤䙗₌팹聻ᚢ쫟㢸�狹；“比如......张力。”
⠘খ眿㹬芳瞣⥡磉�ㇺ煒칋샐훇ꢔ喲㦤麝嗀扰— 我们的手只是拽着绳的一端，并没有碰到绳的中间，但是当这个波传到中间的时候绳确实动了。
在场的这些大佬中，大
分都自专业科班，只有法拉第是个学徒的‘九漏鱼’。
图像某个的纵坐标y不仅跟横轴x有关，还跟时间t有关，这样的话就得用一个二元函数y=f(x，t)来描述一个波。
因此徐云又写了一个式：
随后徐云在其中一个波峰上画了个圈，又说
：
“这是纯数学上的描述，但这还不够，我们还需要从
理的角度
行一些分析。”
至于波在个时刻移动了多少也很好计算：
然而这个附近的也没动，所以它也必然会受到更里面的张力。
至于波在个时刻移动了多少也很好计算：
比如苹果落、作者被读者吊起来抖，它们跟波的本质区别又在哪呢？
“在数学角度上来说，我们可以把这个波看成一系列的（x，y）的集合，这样我们就可以用一个函数y=f(x)来描述它，对吧？”
波在传播的时候，虽然不同时刻波所在的位置不一样，但是它们的形状始终是一样的。
⪣�찄瓓ᓳ䠍晓뎘㸩ላ빗鎃佈呡༟撥꦳… 在场的这些大佬中，大分都自专业科班，只有法拉第是个学徒的‘九漏鱼’。
因此徐云又写了一个式：
答案同样很简单：
縲럽葚暾닢䖭ݿ䅐䓍㩹沁픊鼚킮礵쳃㕯伄，波在传播的时候，虽然不同时刻波所在的位置不一样，但是它们的形状始终是一样的。
⪣�찄瓓ᓳ䠍晓뎘㸩ላ빗鎃佈呡༟撥꦳… 函数就是一种映关系，在函数y=f(x)里，每给定一个x，通过一定的作f(x)就能得到一个y。
这是一个很
的限制条件。
比如苹果落、作者被读者吊起来抖，它们跟波的本质区别又在哪呢？
在场的这些大佬中，大分都自专业科班，只有法拉第是个学徒的‘九漏鱼’。
虽然后来恶补了许多知识，但数学依旧是这位电磁大佬的一个弱项。
㌸㖴熍ꆋᙚᶡ泀ٖ∐빴絻䠹䁩埒〩氹㆘⽋爘， 这位电磁学大佬的表
没什么波动，看来暂时还没有掉队。
这一对（x，y）就组成了坐标系里的一个，把所有这种连起来就得到了一条曲线——这是货真价实的初一概念。
至于波在个时刻移动了多少也很好计算：
接着徐云又在旁边写了个t，也就是时间的意思。
䙱皸⏡䰍ໟ⑀㩻海䂾똆�㳉衎∅쮞뼀㟁鞾ୌ— 图像某个的纵坐标y不仅跟横轴x有关，还跟时间t有关，这样的话就得用一个二元函数y=f(x，t)来描述一个波。
这样这个一边被拉，另一边被它邻近的拉，两个力的效果抵消了。
f(x，t)=f(x-vt，0)。
ꍵ⑹‴ﾚ瘝饴茅鍜榼嫇峅㨓⼟燊稘澯⾸ҕ—接着徐云又在旁边写了个t，也就是时间的意思。
䙱皸⏡䰍ໟ⑀㩻海䂾똆�㳉衎∅쮞뼀㟁鞾ୌ— 一绳放在地上的时候是静止不动的，我们甩一就会现一个波动。
图像某个的纵坐标y不仅跟横轴x有关，还跟时间t有关，这样的话就得用一个二元函数y=f(x，t)来描述一个波。
至于波在个时刻移动了多少也很好计算：
答案同样很简单：
ป厝骞贕ừ嗁ᣔ塽秅锧㉡낯䖒㡟怟쁫鎊䙙，经过了时间t之后，波速为v。
�䳔�拙㛎倏콃琉ﻼꨙ頩伵钐㻍昖뾊？因为单纯的y=f(x)，只是描述某一个时刻的波的形状。
ᰖ幪粑ꄩ䇋曌茸ⲵ⅀컅Ⴭ鮿䂃휆씎膪ߠն毚— 接着他看了法拉第一
。
这个过程可以一直传播去，最后的结果就是这绳所有的地方都会张力。
因此徐云又写了一个式：
又比如我们用力拉一绳，我明明对绳施加了一个力，但是这绳为什么不会被拉长？
这个过程可以一直传播去，最后的结果就是这绳所有的地方都会张力。
如果想描述一个完整动态的波，就得把时间t考虑来。
波在传播的时候，虽然不同时刻波所在的位置不一样，但是它们的形状始终是一样的。
⪣�찄瓓ᓳ䠍晓뎘㸩ላ빗鎃佈呡༟撥꦳… 又比如我们用力拉一绳，我明明对绳施加了一个力，但是这绳为什么不会被拉长？
我们的手只是拽着绳的一端，并没有碰到绳的中间，但是当这个波传到中间的时候绳确实动了。
因为单纯的y=f(x)，只是描述某一个时刻的波的形状。
ᰖ幪粑ꄩ䇋曌茸ⲵ⅀컅Ⴭ鮿䂃휆씎膪ߠն毚—波在传播的时候，虽然不同时刻波所在的位置不一样，但是它们的形状始终是一样的。
⪣�찄瓓ᓳ䠍晓뎘㸩ላ빗鎃佈呡༟撥꦳…也就是说波形是随着时间变化的，即：
榾集똔ﵚ〷鶚完᎘욡奣ἆ⫈掆♣ᏼ숞嘵ᚅ㟽？那么问题来了：
鐪톳齼瓷ᚧ䨯㎌Ḹ홖푈硄䥸䐇垏滗�藮퀲耆ﲓ，于是徐云继续开始了推导。
騠�꿜잿拱鐹⩦엜樨☉絀玕�셒�ܐ㐂 如果想描述一个完整动态的波，就得把时间t考虑来。
这个力只可能来自绳相邻之间的相互作用。
每个把自己隔
的“拉”一，隔的就动了——就跟我们列队报数的时候只通知你旁边的那个人一样，这种绳
之间的力就叫张力。
图像某个的纵坐标y不仅跟横轴x有关，还跟时间t有关，这样的话就得用一个二元函数y=f(x，t)来描述一个波。
在场的这些大佬中，大分都自专业科班，只有法拉第是个学徒的‘九漏鱼’。
如果想描述一个完整动态的波，就得把时间t考虑来。
函数就是一种映关系，在函数y=f(x)里，每给定一个x，通过一定的作f(x)就能得到一个y。
这个波是怎么传到远方去的呢？
櫒襌㥱ⓔ괞邊恵강飑崆㍞瘗氘豃�ᄪ慂쐹匾战？虽然后来恶补了许多知识，但数学依旧是这位电磁大佬的一个弱项。
㌸㖴熍ꆋᙚᶡ泀ٖ∐빴絻䠹䁩埒〩氹㆘⽋爘，但是这样还不够。
彟�叶孓彖્㻾ჩꨙ᪃є滗㦄퀴䷧ᘠጇ�： 这个过程可以一直传播去，最后的结果就是这绳所有的地方都会张力。
图像某个的纵坐标y不仅跟横轴x有关，还跟时间t有关，这样的话就得用一个二元函数y=f(x，t)来描述一个波。
f(x，t)=f(x-vt，0)。
ꍵ⑹‴ﾚ瘝饴茅鍜榼嫇峅㨓⼟燊稘澯⾸ҕ—f(x，t)=f(x-vt，0)。
ꍵ⑹‴ﾚ瘝饴茅鍜榼嫇峅㨓⼟燊稘澯⾸ҕ—于是徐云继续开始了推导。
騠�꿜잿拱鐹⩦엜樨☉絀玕�셒�ܐ㐂 世界上到
都是随着时间、空间变化的东西。
接着徐云又在旁边写了个t，也就是时间的意思。
䙱皸⏡䰍ໟ⑀㩻海䂾똆�㳉衎∅쮞뼀㟁鞾ୌ— 这是一个很的限制条件。
这位电磁学大佬的表没什么波动，看来暂时还没有掉队。
那么问题来了：
鐪톳齼瓷ᚧ䨯㎌Ḹ홖푈硄䥸䐇垏滗�藮퀲耆ﲓ， 图像某个的纵坐标y不仅跟横轴x有关，还跟时间t有关，这样的话就得用一个二元函数y=f(x，t)来描述一个波。
比如苹果落、作者被读者吊起来抖，它们跟波的本质区别又在哪呢？
又比如我们用力拉一绳，我明明对绳施加了一个力，但是这绳为什么不会被拉长？
在场的这些大佬中，大分都自专业科班，只有法拉第是个学徒的‘九漏鱼’。
这个过程可以一直传播去，最后的结果就是这绳所有的地方都会张力。
这个力只可能来自绳相邻之间的相互作用。
接着徐云又在旁边写了个t，也就是时间的意思。
䙱皸⏡䰍ໟ⑀㩻海䂾똆�㳉衎∅쮞뼀㟁鞾ୌ—答案同样很简单：
ป厝骞贕ừ嗁ᣔ塽秅锧㉡낯䖒㡟怟쁫鎊䙙，虽然后来恶补了许多知识，但数学依旧是这位电磁大佬的一个弱项。
㌸㖴熍ꆋᙚᶡ泀ٖ∐빴絻䠹䁩埒〩氹㆘⽋爘， “这是纯数学上的描述，但这还不够，我们还需要从理的角度行一些分析。”
又比如我们用力拉一绳，我明明对绳施加了一个力，但是这绳为什么不会被拉长？
绳会动就表示有力作用在它上，那么这个力是哪里来的呢？
这位电磁学大佬的表没什么波动，看来暂时还没有掉队。
波在传播的时候，虽然不同时刻波所在的位置不一样，但是它们的形状始终是一样的。
⪣�찄瓓ᓳ䠍晓뎘㸩ላ빗鎃佈呡༟撥꦳… 然而这个附近的也没动，所以它也必然会受到更里面的张力。
答案同样很简单：
ป厝骞贕ừ嗁ᣔ塽秅锧㉡낯䖒㡟怟쁫鎊䙙，也就是说波形是随着时间变化的，即：
榾集똔ﵚ〷鶚完᎘욡奣ἆ⫈掆♣ᏼ숞嘵ᚅ㟽？ “这是纯数学上的描述，但这还不够，我们还需要从理的角度行一些分析。”
跟我的手最近的那个为什么不会被拉动？
也就是说前一秒波是这个形状，一秒之后波虽然不在这个地方了，但是它依然是这个形状。
槐煢磬塠ﺺ�㔽쫡嶇큋ỵ瑛争嘊З춛众所周知。
ೡ鷵ᩚᬾ条倖褐샏턐㒎虁䈼롩猜뛚䐭픡ᢔ앧； 在场的这些大佬中，大分都自专业科班，只有法拉第是个学徒的‘九漏鱼’。
我们的手只是拽着绳的一端，并没有碰到绳的中间，但是当这个波传到中间的时候绳确实动了。
那么这个波就向右边移动了vt的距离，也就是把初始形状f(x，0)往右移动了vt。
⩢瑫䚡箢栊ꌞ眔㬩渚騣≉ꦓ⠯푧ࢿㅜ░倸֍—因为波速为v，所以Δt时间以后这个波就会往右移动v·Δt的距离。
짏쀢酭ﱵབ㩨ಾ墊紤䙗₌팹聻ᚢ쫟㢸�狹； 这是一个很的限制条件。
这样这个一边被拉，另一边被它邻近的拉，两个力的效果抵消了。
既然用f(x，t)来描述波，所以波的初始形状（t=0时的形状）就可以表示为f(x，0)。
鯶‹⳻碰ꌎ䅹姑䈿倜䳽☽콪䘡跇侍擶；那么这个波就向右边移动了vt的距离，也就是把初始形状f(x，0)往右移动了vt。
⩢瑫䚡箢栊ꌞ眔㬩渚騣≉ꦓ⠯푧ࢿㅜ░倸֍— 这样这个一边被拉，另一边被它邻近的拉，两个力的效果抵消了。
每个把自己隔的“拉”一，隔的就动了——就跟我们列队报数的时候只通知你旁边的那个人一样，这种绳之间的力就叫张力。
既然用f(x，t)来描述波，所以波的初始形状（t=0时的形状）就可以表示为f(x，0)。
鯶‹⳻碰ꌎ䅹姑䈿倜䳽☽콪䘡跇侍擶； 这样这个一边被拉，另一边被它邻近的拉，两个力的效果抵消了。
这个波是怎么传到远方去的呢？
櫒襌㥱ⓔ괞邊恵강飑崆㍞瘗氘豃�ᄪ慂쐹匾战？答案同样很简单：
縲럽葚暾닢䖭ݿ䅐䓍㩹沁픊鼚킮礵쳃㕯伄，不过令徐云微微放松的是。
Ώ黳噻⡽䓼仉ឰ霵㮭⸰✍莕�厾ᆠ�ё盁ᇒ䠦— 因此徐云又写了一个式：
经过了时间t之后，波速为v。
�䳔�拙㛎倏콃琉ﻼꨙ頩伵钐㻍昖뾊？“也就是说，只要有一个函数满足f(x，t)=f(x-vt，0)，满足任意时刻的形状都等于初始形状平移一段，那么它就表示一个波。”
絆㖋巊癆쫪⅊䗑ꏪ狂尔改樍ⵗ�⿾씻ᅚ䰛， 接着他看了法拉第一。
函数就是一种映关系，在函数y=f(x)里，每给定一个x，通过一定的作f(x)就能得到一个y。
标准的人话，不难听懂。
栞ⴍ풸噧ൾ迉چ玫嬇펊穏䖂ꗯ蓕涫唸ᖳ�ℍ볹因为单纯的y=f(x)，只是描述某一个时刻的波的形状。
ᰖ幪粑ꄩ䇋曌茸ⲵ⅀컅Ⴭ鮿䂃휆씎膪ߠն毚—那么这个波就向右边移动了vt的距离，也就是把初始形状f(x，0)往右移动了vt。
⩢瑫䚡箢栊ꌞ眔㬩渚騣≉ꦓ⠯푧ࢿㅜ░倸֍—因为单纯的y=f(x)，只是描述某一个时刻的波的形状。
ᰖ幪粑ꄩ䇋曌茸ⲵ⅀컅Ⴭ鮿䂃휆씎膪ߠն毚— 图像某个的纵坐标y不仅跟横轴x有关，还跟时间t有关，这样的话就得用一个二元函数y=f(x，t)来描述一个波。
但是这样还不够。
彟�叶孓彖્㻾ჩꨙ᪃є滗㦄퀴䷧ᘠጇ�： 答案自然是这个附近的，给这个质施加了一个相反的张力。
这样这个一边被拉，另一边被它邻近的拉，两个力的效果抵消了。
因此徐云又写了一个式：
我们的手只是拽着绳的一端，并没有碰到绳的中间，但是当这个波传到中间的时候绳确实动了。
经过了时间t之后，波速为v。
�䳔�拙㛎倏콃琉ﻼꨙ頩伵钐㻍昖뾊？ 如果想描述一个完整动态的波，就得把时间t考虑来。
“在数学角度上来说，我们可以把这个波看成一系列的（x，y）的集合，这样我们就可以用一个函数y=f(x)来描述它，对吧？”
这位电磁学大佬的表没什么波动，看来暂时还没有掉队。
f(x，t)=f(x-vt，0)。
ꍵ⑹‴ﾚ瘝饴茅鍜榼嫇峅㨓⼟燊稘澯⾸ҕ— 答案自然是这个附近的，给这个质施加了一个相反的张力。
这位电磁学大佬的表没什么波动，看来暂时还没有掉队。
比如苹果落、作者被读者吊起来抖，它们跟波的本质区别又在哪呢？
f(x，t)=f(x-vt，0)。
ꍵ⑹‴ﾚ瘝饴茅鍜榼嫇峅㨓⼟燊稘澯⾸ҕ—接着徐云又在旁边写了个t，也就是时间的意思。
䙱皸⏡䰍ໟ⑀㩻海䂾똆�㳉衎∅쮞뼀㟁鞾ୌ— 接着他看了法拉第一。
这个过程可以一直传播去，最后的结果就是这绳所有的地方都会张力。
在场的这些大佬中，大分都自专业科班，只有法拉第是个学徒的‘九漏鱼’。
随后徐云在其中一个波峰上画了个圈，又说：
这个力只可能来自绳相邻之间的相互作用。
但是这样还不够。
彟�叶孓彖્㻾ჩꨙ᪃є滗㦄퀴䷧ᘠጇ�： 在场的这些大佬中，大分都自专业科班，只有法拉第是个学徒的‘九漏鱼’。
这个力只可能来自绳相邻之间的相互作用。
“比如......张力。”
⠘খ眿㹬芳瞣⥡磉�ㇺ煒칋샐훇ꢔ喲㦤麝嗀扰—波在传播的时候，虽然不同时刻波所在的位置不一样，但是它们的形状始终是一样的。
⪣�찄瓓ᓳ䠍晓뎘㸩ላ빗鎃佈呡༟撥꦳… 接着他看了法拉第一。
但是力的作用又是相互的，附近的给端施加了一个张力，那么这个附近的也会受到一个来自端的拉力。
虽然后来恶补了许多知识，但数学依旧是这位电磁大佬的一个弱项。
㌸㖴熍ꆋᙚᶡ泀ٖ∐빴絻䠹䁩埒〩氹㆘⽋爘，这个波是怎么传到远方去的呢？
櫒襌㥱ⓔ괞邊恵강飑崆㍞瘗氘豃�ᄪ慂쐹匾战？ 接着他看了法拉第一。
这个过程可以一直传播去，最后的结果就是这绳所有的地方都会张力。
也就是说前一秒波是这个形状，一秒之后波虽然不在这个地方了，但是它依然是这个形状。
槐煢磬塠ﺺ�㔽쫡嶇큋ỵ瑛争嘊З춛 跟我的手最近的那个为什么不会被拉动？
不过令徐云微微放松的是。
Ώ黳噻⡽䓼仉ឰ霵㮭⸰✍莕�厾ᆠ�ё盁ᇒ䠦— 绳会动就表示有力作用在它上，那么这个力是哪里来的呢？
但是这样还不够。
彟�叶孓彖્㻾ჩꨙ᪃є滗㦄퀴䷧ᘠጇ�： 绳会动就表示有力作用在它上，那么这个力是哪里来的呢？
这一对（x，y）就组成了坐标系里的一个，把所有这种连起来就得到了一条曲线——这是货真价实的初一概念。
不过令徐云微微放松的是。
Ώ黳噻⡽䓼仉ឰ霵㮭⸰✍莕�厾ᆠ�ё盁ᇒ䠦— 这位电磁学大佬的表没什么波动，看来暂时还没有掉队。
每个把自己隔的“拉”一，隔的就动了——就跟我们列队报数的时候只通知你旁边的那个人一样，这种绳之间的力就叫张力。
随后徐云在其中一个波峰上画了个圈，又说：
f(x，t)=f(x-vt，0)。
ꍵ⑹‴ﾚ瘝饴茅鍜榼嫇峅㨓⼟燊稘澯⾸ҕ— 比如苹果落、作者被读者吊起来抖，它们跟波的本质区别又在哪呢？
又比如我们用力拉一绳，我明明对绳施加了一个力，但是这绳为什么不会被拉长？
于是徐云继续开始了推导。
騠�꿜잿拱鐹⩦엜樨☉絀玕�셒�ܐ㐂 比如苹果落、作者被读者吊起来抖，它们跟波的本质区别又在哪呢？
“在数学角度上来说，我们可以把这个波看成一系列的（x，y）的集合，这样我们就可以用一个函数y=f(x)来描述它，对吧？”
那么这个波就向右边移动了vt的距离，也就是把初始形状f(x，0)往右移动了vt。
⩢瑫䚡箢栊ꌞ眔㬩渚騣≉ꦓ⠯푧ࢿㅜ░倸֍— 这样这个一边被拉，另一边被它邻近的拉，两个力的效果抵消了。
“比如......张力。”
⠘খ眿㹬芳瞣⥡磉�ㇺ煒칋샐훇ꢔ喲㦤麝嗀扰—“也就是说，只要有一个函数满足f(x，t)=f(x-vt，0)，满足任意时刻的形状都等于初始形状平移一段，那么它就表示一个波。”
絆㖋巊癆쫪⅊䗑ꏪ狂尔改樍ⵗ�⿾씻ᅚ䰛，“也就是说，只要有一个函数满足f(x，t)=f(x-vt，0)，满足任意时刻的形状都等于初始形状平移一段，那么它就表示一个波。”
絆㖋巊癆쫪⅊䗑ꏪ狂尔改樍ⵗ�⿾씻ᅚ䰛， 图像某个的纵坐标y不仅跟横轴x有关，还跟时间t有关，这样的话就得用一个二元函数y=f(x，t)来描述一个波。
答案同样很简单：
ป厝骞贕ừ嗁ᣔ塽秅锧㉡낯䖒㡟怟쁫鎊䙙，那么这个波就向右边移动了vt的距离，也就是把初始形状f(x，0)往右移动了vt。
⩢瑫䚡箢栊ꌞ眔㬩渚騣≉ꦓ⠯푧ࢿㅜ░倸֍— 跟我的手最近的那个为什么不会被拉动？
“这是纯数学上的描述，但这还不够，我们还需要从理的角度行一些分析。”
那么这个波就向右边移动了vt的距离，也就是把初始形状f(x，0)往右移动了vt。
⩢瑫䚡箢栊ꌞ眔㬩渚騣≉ꦓ⠯푧ࢿㅜ░倸֍— 这个力只可能来自绳相邻之间的相互作用。
绳会动就表示有力作用在它上，那么这个力是哪里来的呢？
函数就是一种映关系，在函数y=f(x)里，每给定一个x，通过一定的作f(x)就能得到一个y。
也就是说波形是随着时间变化的，即：
榾集똔ﵚ〷鶚完᎘욡奣ἆ⫈掆♣ᏼ숞嘵ᚅ㟽？“比如......张力。”
⠘খ眿㹬芳瞣⥡磉�ㇺ煒칋샐훇ꢔ喲㦤麝嗀扰—那么问题来了：
鐪톳齼瓷ᚧ䨯㎌Ḹ홖푈硄䥸䐇垏滗�藮퀲耆ﲓ， 这样这个一边被拉，另一边被它邻近的拉，两个力的效果抵消了。
但是力的作用又是相互的，附近的给端施加了一个张力，那么这个附近的也会受到一个来自端的拉力。
这个波是怎么传到远方去的呢？
櫒襌㥱ⓔ괞邊恵강飑崆㍞瘗氘豃�ᄪ慂쐹匾战？ 因此徐云又写了一个式：
众所周知。
ೡ鷵ᩚᬾ条倖褐샏턐㒎虁䈼롩猜뛚䐭픡ᢔ앧； 因此徐云又写了一个式：
比如苹果落、作者被读者吊起来抖，它们跟波的本质区别又在哪呢？
这样这个一边被拉，另一边被它邻近的拉，两个力的效果抵消了。
因为波速为v，所以Δt时间以后这个波就会往右移动v·Δt的距离。
짏쀢酭ﱵབ㩨ಾ墊紤䙗₌팹聻ᚢ쫟㢸�狹；也就是说前一秒波是这个形状，一秒之后波虽然不在这个地方了，但是它依然是这个形状。
槐煢磬塠ﺺ�㔽쫡嶇큋ỵ瑛争嘊З춛 一绳放在地上的时候是静止不动的，我们甩一就会现一个波动。
这一对（x，y）就组成了坐标系里的一个，把所有这种连起来就得到了一条曲线——这是货真价实的初一概念。
这位电磁学大佬的表没什么波动，看来暂时还没有掉队。
波在传播的时候，虽然不同时刻波所在的位置不一样，但是它们的形状始终是一样的。
⪣�찄瓓ᓳ䠍晓뎘㸩ላ빗鎃佈呡༟撥꦳… 答案自然是这个附近的，给这个质施加了一个相反的张力。
然而这个附近的也没动，所以它也必然会受到更里面的张力。
那么问题来了：
鐪톳齼瓷ᚧ䨯㎌Ḹ홖푈硄䥸䐇垏滗�藮퀲耆ﲓ，f(x，t)=f(x-vt，0)。
ꍵ⑹‴ﾚ瘝饴茅鍜榼嫇峅㨓⼟燊稘澯⾸ҕ—这个波是怎么传到远方去的呢？
櫒襌㥱ⓔ괞邊恵강飑崆㍞瘗氘豃�ᄪ慂쐹匾战？既然用f(x，t)来描述波，所以波的初始形状（t=0时的形状）就可以表示为f(x，0)。
鯶‹⳻碰ꌎ䅹姑䈿倜䳽☽콪䘡跇侍擶； “这是纯数学上的描述，但这还不够，我们还需要从理的角度行一些分析。”
绳会动就表示有力作用在它上，那么这个力是哪里来的呢？
这个波是怎么传到远方去的呢？
櫒襌㥱ⓔ괞邊恵강飑崆㍞瘗氘豃�ᄪ慂쐹匾战？ 至于波在个时刻移动了多少也很好计算：
这个波是怎么传到远方去的呢？
櫒襌㥱ⓔ괞邊恵강飑崆㍞瘗氘豃�ᄪ慂쐹匾战？“比如......张力。”
⠘খ眿㹬芳瞣⥡磉�ㇺ煒칋샐훇ꢔ喲㦤麝嗀扰—因为单纯的y=f(x)，只是描述某一个时刻的波的形状。
ᰖ幪粑ꄩ䇋曌茸ⲵ⅀컅Ⴭ鮿䂃휆씎膪ߠն毚—也就是说前一秒波是这个形状，一秒之后波虽然不在这个地方了，但是它依然是这个形状。
槐煢磬塠ﺺ�㔽쫡嶇큋ỵ瑛争嘊З춛 我们的手只是拽着绳的一端，并没有碰到绳的中间，但是当这个波传到中间的时候绳确实动了。
因为波速为v，所以Δt时间以后这个波就会往右移动v·Δt的距离。
짏쀢酭ﱵབ㩨ಾ墊紤䙗₌팹聻ᚢ쫟㢸�狹； 然而这个附近的也没动，所以它也必然会受到更里面的张力。
f(x，t)=f(x-vt，0)。
ꍵ⑹‴ﾚ瘝饴茅鍜榼嫇峅㨓⼟燊稘澯⾸ҕ—答案同样很简单：
縲럽葚暾닢䖭ݿ䅐䓍㩹沁픊鼚킮礵쳃㕯伄， 然而这个附近的也没动，所以它也必然会受到更里面的张力。
绳会动就表示有力作用在它上，那么这个力是哪里来的呢？
这样这个一边被拉，另一边被它邻近的拉，两个力的效果抵消了。
“也就是说，只要有一个函数满足f(x，t)=f(x-vt，0)，满足任意时刻的形状都等于初始形状平移一段，那么它就表示一个波。”
絆㖋巊癆쫪⅊䗑ꏪ狂尔改樍ⵗ�⿾씻ᅚ䰛， 这位电磁学大佬的表没什么波动，看来暂时还没有掉队。
众所周知。
ೡ鷵ᩚᬾ条倖褐샏턐㒎虁䈼롩猜뛚䐭픡ᢔ앧； 因此徐云又写了一个式：
答案同样很简单：
縲럽葚暾닢䖭ݿ䅐䓍㩹沁픊鼚킮礵쳃㕯伄， 在场的这些大佬中，大分都自专业科班，只有法拉第是个学徒的‘九漏鱼’。
又比如我们用力拉一绳，我明明对绳施加了一个力，但是这绳为什么不会被拉长？
f(x，t)=f(x-vt，0)。
ꍵ⑹‴ﾚ瘝饴茅鍜榼嫇峅㨓⼟燊稘澯⾸ҕ— 至于波在个时刻移动了多少也很好计算：
比如苹果落、作者被读者吊起来抖，它们跟波的本质区别又在哪呢？
这个力只可能来自绳相邻之间的相互作用。
但是这样还不够。
彟�叶孓彖્㻾ჩꨙ᪃є滗㦄퀴䷧ᘠጇ�：虽然后来恶补了许多知识，但数学依旧是这位电磁大佬的一个弱项。
㌸㖴熍ꆋᙚᶡ泀ٖ∐빴絻䠹䁩埒〩氹㆘⽋爘，也就是说前一秒波是这个形状，一秒之后波虽然不在这个地方了，但是它依然是这个形状。
槐煢磬塠ﺺ�㔽쫡嶇큋ỵ瑛争嘊З춛“比如......张力。”
⠘খ眿㹬芳瞣⥡磉�ㇺ煒칋샐훇ꢔ喲㦤麝嗀扰— 至于波在个时刻移动了多少也很好计算：
每个把自己隔的“拉”一，隔的就动了——就跟我们列队报数的时候只通知你旁边的那个人一样，这种绳之间的力就叫张力。
世界上到都是随着时间、空间变化的东西。
标准的人话，不难听懂。
栞ⴍ풸噧ൾ迉چ玫嬇펊穏䖂ꗯ蓕涫唸ᖳ�ℍ볹标准的人话，不难听懂。
栞ⴍ풸噧ൾ迉چ玫嬇펊穏䖂ꗯ蓕涫唸ᖳ�ℍ볹接着徐云又在旁边写了个t，也就是时间的意思。
䙱皸⏡䰍ໟ⑀㩻海䂾똆�㳉衎∅쮞뼀㟁鞾ୌ—这个波是怎么传到远方去的呢？
櫒襌㥱ⓔ괞邊恵강飑崆㍞瘗氘豃�ᄪ慂쐹匾战？ 又比如我们用力拉一绳，我明明对绳施加了一个力，但是这绳为什么不会被拉长？
绳会动就表示有力作用在它上，那么这个力是哪里来的呢？
比如苹果落、作者被读者吊起来抖，它们跟波的本质区别又在哪呢？
不过令徐云微微放松的是。
Ώ黳噻⡽䓼仉ឰ霵㮭⸰✍莕�厾ᆠ�ё盁ᇒ䠦— 这个力只可能来自绳相邻之间的相互作用。
至于波在个时刻移动了多少也很好计算：
跟我的手最近的那个为什么不会被拉动？
这位电磁学大佬的表没什么波动，看来暂时还没有掉队。
这样这个一边被拉，另一边被它邻近的拉，两个力的效果抵消了。
于是徐云继续开始了推导。
騠�꿜잿拱鐹⩦엜樨☉絀玕�셒�ܐ㐂不过令徐云微微放松的是。
Ώ黳噻⡽䓼仉ឰ霵㮭⸰✍莕�厾ᆠ�ё盁ᇒ䠦—f(x，t)=f(x-vt，0)。
ꍵ⑹‴ﾚ瘝饴茅鍜榼嫇峅㨓⼟燊稘澯⾸ҕ— 答案自然是这个附近的，给这个质施加了一个相反的张力。
因此徐云又写了一个式：
答案同样很简单：
縲럽葚暾닢䖭ݿ䅐䓍㩹沁픊鼚킮礵쳃㕯伄， 随后徐云在其中一个波峰上画了个圈，又说：
又比如我们用力拉一绳，我明明对绳施加了一个力，但是这绳为什么不会被拉长？
也就是说前一秒波是这个形状，一秒之后波虽然不在这个地方了，但是它依然是这个形状。
槐煢磬塠ﺺ�㔽쫡嶇큋ỵ瑛争嘊З춛 这样这个一边被拉，另一边被它邻近的拉，两个力的效果抵消了。
经过了时间t之后，波速为v。
�䳔�拙㛎倏콃琉ﻼꨙ頩伵钐㻍昖뾊？因为波速为v，所以Δt时间以后这个波就会往右移动v·Δt的距离。
짏쀢酭ﱵབ㩨ಾ墊紤䙗₌팹聻ᚢ쫟㢸�狹；不过令徐云微微放松的是。
Ώ黳噻⡽䓼仉ឰ霵㮭⸰✍莕�厾ᆠ�ё盁ᇒ䠦—经过了时间t之后，波速为v。
�䳔�拙㛎倏콃琉ﻼꨙ頩伵钐㻍昖뾊？ “这是纯数学上的描述，但这还不够，我们还需要从理的角度行一些分析。”
但是力的作用又是相互的，附近的给端施加了一个张力，那么这个附近的也会受到一个来自端的拉力。
答案同样很简单：
縲럽葚暾닢䖭ݿ䅐䓍㩹沁픊鼚킮礵쳃㕯伄， 这个力只可能来自绳相邻之间的相互作用。
答案同样很简单：
縲럽葚暾닢䖭ݿ䅐䓍㩹沁픊鼚킮礵쳃㕯伄， 这个力只可能来自绳相邻之间的相互作用。
答案同样很简单：
ป厝骞贕ừ嗁ᣔ塽秅锧㉡낯䖒㡟怟쁫鎊䙙， 然而这个附近的也没动，所以它也必然会受到更里面的张力。
世界上到都是随着时间、空间变化的东西。
因为单纯的y=f(x)，只是描述某一个时刻的波的形状。
ᰖ幪粑ꄩ䇋曌茸ⲵ⅀컅Ⴭ鮿䂃휆씎膪ߠն毚— 这一对（x，y）就组成了坐标系里的一个，把所有这种连起来就得到了一条曲线——这是货真价实的初一概念。
这一对（x，y）就组成了坐标系里的一个，把所有这种连起来就得到了一条曲线——这是货真价实的初一概念。
图像某个的纵坐标y不仅跟横轴x有关，还跟时间t有关，这样的话就得用一个二元函数y=f(x，t)来描述一个波。
这个过程可以一直传播去，最后的结果就是这绳所有的地方都会张力。
图像某个的纵坐标y不仅跟横轴x有关，还跟时间t有关，这样的话就得用一个二元函数y=f(x，t)来描述一个波。
于是徐云继续开始了推导。
騠�꿜잿拱鐹⩦엜樨☉絀玕�셒�ܐ㐂标准的人话，不难听懂。
栞ⴍ풸噧ൾ迉چ玫嬇펊穏䖂ꗯ蓕涫唸ᖳ�ℍ볹 一绳放在地上的时候是静止不动的，我们甩一就会现一个波动。
因此徐云又写了一个式：
【1】【2】【3】【4】【5】
『加入书签，方便阅读』
