第二百五十七章 见证奇迹吧!(上)
(θ Δθ)-t·tanθ=μ·Δxa?2f/?t2。】
“稍等一 。”
。”
看到这句话,法拉第忽然皱起了眉 ,打断了徐云。
,打断了徐云。
很明显。
此时他已经隐隐 现了掉队的迹象:
现了掉队的迹象:
“罗峰同学,用tanθ替代sinθ的意义是什么?”
徐云又看了小麦,小麦当即心领神会:
“法拉第先生,因为正切值tanθ还可以代表一条直线的斜率呀,也就是代表曲线在某一 的导数。”
的导数。”
“正切值的表达式是tanθ=c/b,如果建一个坐标系,那么这个c刚好就是直线在y轴的投影dy,b就是在x轴的投影dx。”
“它们的比值刚好就是导数dy/dx,也就是说tanθ=dy/dx。”
法拉第认真听完,花了两分钟在纸上演算了一番,旋即恍然的一拍额 :
:
“原来如此,我明白了,请继续吧,罗峰同学。”
徐云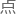
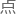
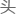 ,继续解释
,继续解释 :
:
“因为波的函数f(x,t)是关于x和t的二元函数,所以我们只能求某一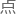 的偏导数。”
的偏导数。”
“那么正切值就等于它在这个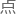 的偏导数tanθ=?f/?x,原来的波动方程就可以写成这样......”
的偏导数tanθ=?f/?x,原来的波动方程就可以写成这样......”
随后徐云在纸上写 了一个新方程:
了一个新方程:
t(?f/?xlx △x-?f/?xlx)=μ·Δxa?2f/?t2。
看起来比之前的要复杂一些,但现场的这些大佬的目光,却齐齐明亮了不少。
到了这一步,接 来的思路就很清晰了。
来的思路就很清晰了。
只要再对方程的两边同时除以Δx,那左边就变成了函数?f/?x在x Δx和x这两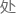 的值的差除以Δx。
的值的差除以Δx。
这其实就是?f/?x这个函数的导数表达式。
也就是说。
两边同时除以一个Δx之后,左边就变成了偏导数?f/?x对x再求一次导数,那就是f(x,t)对x求二阶偏导数了。
同时上面已经用?2f/?t2来表示函数对t的二阶偏导数,那么这里自然就可以用?2f/?x2来表示函数对x的二阶偏导数。
然后两边再同时除以t,得到方程就简洁多了:
?2f/?x=μ?2f/t?x2。
同时如果你脑 还没晕的话便会发现.....
还没晕的话便会发现.....
μ/t的单位.....
刚好就是速度平方的倒数!
也就是说如果我们把一个量定义成t/μ的平方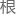 ,那么这个量的单位刚好就是速度的单位。
,那么这个量的单位刚好就是速度的单位。
可以想象,这个速度自然就是这个波的传播速度v:
v2=t/μ。
因此将这个值代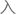 之后,一个最终的公式便
之后,一个最终的公式便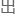 现了:
现了:
?2f/?x=?2f/v2?x2。
这个公式在后世又叫 ......
......
经典波动方程。
当然了。
这个方程没有没有考虑量 效应。
效应。
如果要考虑量 效应,这个经典的波动方程就没用了,就必须转而使用量
效应,这个经典的波动方程就没用了,就必须转而使用量 的波动方程,那就是大名鼎鼎的薛定谔方程。
的波动方程,那就是大名鼎鼎的薛定谔方程。
薛定谔就是从这个经典波动方程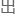 发,结合德布罗意的
发,结合德布罗意的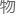 质波概念,
质波概念,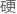 猜
猜 了薛定谔方程。
了薛定谔方程。
没错,靠猜的。


 容就先不赘述了,总之这个方程让
容就先不赘述了,总之这个方程让 理学家们从被海森堡的矩阵支
理学家们从被海森堡的矩阵支 的恐惧中解脱了
的恐惧中解脱了 来,重新回到了微分方程的
来,重新回到了微分方程的 好世界。
好世界。
如今徐云不需要考虑量 方面的事儿,因此有经典波动方程就足够了。
方面的事儿,因此有经典波动方程就足够了。
接着他又在纸上写 了一
了一 新的公式。
新的公式。
而随着这 新公式的写
新公式的写 ,法拉第赫然发现......
,法拉第赫然发现......
自己剩 的那一片硝酸甘油,好像不太够用了。
的那一片硝酸甘油,好像不太够用了。
..........
注:
有人说伏特是我给bug打的补丁,无语....我会犯这种常识 的错误吗,之前泰勒展开我都用韩立展开替代了,光伏这个写
的错误吗,之前泰勒展开我都用韩立展开替代了,光伏这个写 来这么久没改还不能说明啥嘛。
来这么久没改还不能说明啥嘛。
类似的伏笔我之前又不是没写过,甚至我在《来夫剑诀》那章就说过这个功法 一个副本会用到,当时就已经把小麦副本设计好了。
一个副本会用到,当时就已经把小麦副本设计好了。
留 来的线被说成打补丁,一言难尽.jpg。
来的线被说成打补丁,一言难尽.jpg。
【1】【2】【3】【4】【5】
『加入书签,方便阅读』


