者就相当了：

        他叫凯文・哈士奇――这是个真人，英文写作Husky，没有任何音译上的加工。

        第三种则是介质分拖动以太。

        也就是菲涅尔的分曳引假说，于1818年提，堪称赫赫有名。

        完全拖动以太和完全不拖动以太都好理解，就是字面上的意思。

        前者认为运动介质在以太中运动就像推土机推土那般，会在“前”的时候把以太全推走。

        后者则认为就像纱网在里运动一样，对以太完全没影响。

        事实上。

        1850年影响最大的其实是第三种，也就是菲涅尔的分曳引假说。

        也就是认为运动介质在以太中运动，它既不是一不，也不是把以太全打包拖走，而是只拖走一分。

        拖走多少呢？

        菲涅尔认为这跟介质的折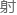率有关。

        折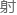率越大，拖着的以太就越多。

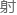        的拖曳系数是1-1/n2――n是介质的折率。

        比如空气的折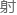率大约是1，那么空气的拖曳系数就是1-1/1=0。

        也就是说空气并不会拖曳以太。

        的折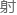率大约是1.33，那么的拖曳系数大约是1-1/1.332≈0.43。

        也就是说。

        如果以速度v相对以太运动，就会拖着以太以0.43v的速度运动。

        这个说法不难理解，但它在后世衍生了不知多少的妖鬼怪。（烈建议这里个，面这段容可以说是后世90%理民科提各种理论的源）

        因为在菲涅尔提这个理论之后，斐索....也就是测算光速的那位天才，又想了个实验。

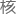        斐索实验的心很简单：

        就是让一束光顺运动，另一束光逆运动，二者方向相反。

        然后通过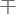涉图案，来测量它们因为速度不同导致的时间差。

        不过菲涅尔并没有使用两束光，而是利用一个弯曲的就达到了目的。

        为什么会有时间差呢？

        上面说过。

        据菲涅尔的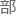分曳引假说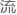，在运动的时候，会就会拖着以太以0.43v的速度运动。

        而如果以太在运动，那么光的速度当然也会跟着变化。

        光在真空中的速度是c，在中的速度就是。

        不难想象。

        如果光线逆着运动，那么地面上观测的速度就是光在中的速度减去以太被拖曳的速度ku。

        也就是()-ku。

        同理。

        顺运动光线的速度就应该是光在中的速度，加上以太被拖曳的速度ku。

        也就是()  ku。

        在这种况。