第三百二十章 玩的可真特么大(下)(万字更新!!!)
“我们可以在两条光束的尽 各放置一面反光镜,如此一来,就像当初罗峰先生测定光速那样,两
各放置一面反光镜,如此一来,就像当初罗峰先生测定光速那样,两 光碰到反光镜后会发生反
光碰到反光镜后会发生反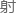 ,
,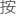 照来时的方向返回分光镜。”
照来时的方向返回分光镜。”
“接着再在垂直光路的另一侧...也就是黑板的 方再放置一块观测屏。”
方再放置一块观测屏。”
“那么光束1便会先经反光镜m1反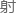 、再经分光镜投
、再经分光镜投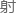 到观测屏。”
到观测屏。”
“光束2同理,经反光镜m2反 再经分光镜投
再经分光镜投 到观测屏,与光束1形成
到观测屏,与光束1形成 涉.......”
涉.......”
小麦的思路显然要比休伯特・艾里完整许多,从动笔书写开始,他握着的粉笔便没有停 来过。
来过。
台 无论是大一、大四还是研一研三,所有人都聚
无论是大一、大四还是研一研三,所有人都聚 会神的看着小麦的演示。
会神的看着小麦的演示。
哒哒哒――
整个活动室 一片寂静,只有粉笔与黑板的接
一片寂静,只有粉笔与黑板的接 声与小麦的解释声,连徐云都退到了一旁:
声与小麦的解释声,连徐云都退到了一旁:
“......接着我们再让实验仪 整
整 旋转90度,则光束1和光束2到达观测屏的时间互换,使得已经形成的
旋转90度,则光束1和光束2到达观测屏的时间互换,使得已经形成的 涉条纹产生移动。”
涉条纹产生移动。”
“当整个仪 缓慢转动时连续读数,如果我们的设备
缓慢转动时连续读数,如果我们的设备 度很
度很 ,那么测
,那么测 条纹移动应该是很容易的事
条纹移动应该是很容易的事 .......”
.......”
“....... 涉条纹如果发生了移动,从实验中测
涉条纹如果发生了移动,从实验中测 条纹移动的距离,就可以求
条纹移动的距离,就可以求 地球相对以太的运动速度,从而证实以太的存在。”
地球相对以太的运动速度,从而证实以太的存在。”
早先提及过。
现场的社员们除了布鲁赫这种个例之外,大多数都是自然科学的 好者。
好者。
虽然他们掌握的知识纯度与深度无法和后世的同龄人相比,但基础的理科素养还是 备的。
备的。
因此随着小麦的板书逐渐填满黑板,台 也陆续有社员脸上
也陆续有社员脸上
 了恍然的表
了恍然的表 。
。
甚至还有不少人拿 笔记,一边记录
笔记,一边记录 方案,一边带
方案,一边带 数值计算了起来。
数值计算了起来。
没错。
想必有些不丢脸同学也已经看 来了。
来了。
徐云这次引导格 社设计的实验,正是20世纪
社设计的实验,正是20世纪 理学大名鼎鼎的两大乌云之一......
理学大名鼎鼎的两大乌云之一......
迈克尔逊-莫雷实验!
这是1887年迈克尔逊和莫雷在老鹰那边
 来的一个著名实验,它的思路其实很简单,也就是徐云此前说过的那番话:
来的一个著名实验,它的思路其实很简单,也就是徐云此前说过的那番话:
如果存在以太,则当地球穿过以太绕太阳公转时,在地球通过以太运动的方向测量的光速,应该大于在与运动垂直方向测量的光速。
于是呢,
迈克尔逊和莫雷他们就搞 了这么个实验设备。
了这么个实验设备。
这个实验使用到的仪 并不复杂,从俯视图来看,总共分成四个模块:
并不复杂,从俯视图来看,总共分成四个模块:
光源位于俯视图的最左边,光路从左往右发 ――在实际
――在实际 作的时候,这个方向要与地球公转的方向一致。
作的时候,这个方向要与地球公转的方向一致。
光源右侧的位置上放着一块分光镜。
分光镜字如其名,就是可以将光线分开的镜 ,也叫作分束镜。
,也叫作分束镜。
它从材料的 质上划分是一种镀膜玻璃,在光学玻璃表面镀上一层或多层薄膜。
质上划分是一种镀膜玻璃,在光学玻璃表面镀上一层或多层薄膜。
当一束光投 到镀膜玻璃上后,通过反
到镀膜玻璃上后,通过反 和折
和折 ,光束就被分为两束或更多束。
,光束就被分为两束或更多束。
迈克尔逊莫雷实验需要用到的分光镜的 度要求很
度要求很 ,它可以将光线分成继续向右的光束1,以及垂直向上的光束2――同样是俯视图的说法。
,它可以将光线分成继续向右的光束1,以及垂直向上的光束2――同样是俯视图的说法。
随后在光束1和光束2的末端再放置两块反光镜,光线抵达后便会原路返回。
早先说过。
地球公转的时候会有迎面 来的‘以太风’,这个速度是30公里每秒。
来的‘以太风’,这个速度是30公里每秒。
因此在沿着公转方向上的光束1,到达m1和从m1返回的传播速度为不同的。
假设地球的速度是v,分光镜到反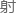 镜的距离是d。
镜的距离是d。
那么过去和回来的速度就分别是c-v和c v,相当于逆风和顺丰。